Raciocine

Deixe suas respostas em forma de comentários.

1 - Um pastor diz para outro: "Dê um de seus carneiros que ficamos com igual número de carneiros." O outro responde: "Nada disso, dê-me um de seus carneiros que ficarei com o dobro dos seus". Quantos carneiros têm cada um?

2 - Uma lesma deve subir um poste de 10 metros de altura. De dia sobe 2m e à noite desce 1m. Em quantos dias atingirá o topo do poste?

3 - Três gatos comem três ratos em três minutos. Cem gatos comem cem ratos em quantos minutos?

4 - O pai do padre é filho do meu pai. O que eu sou do Padre?

5 - Qual é o dobro da metade de dois?

6 - Se um bezerro pesa 75 kg mais meio bezerro, quanto pesa um bezerro inteiro?

7 - Um avião lotado de passageiros parte do Rio de Janeiro em direção a Buenos Aires. Por uma fatalidade cai na fronteira Brasil-Argentina. Onde serão enterrados os sobreviventes?

8 - 200 burros estão andando em fila, um burro cai ele olha paras trás, quantos burros ele vai contar?

9 - Qual é a metade de dois mais dois?

10 - Uma pata nascida no Chile bota um ovo na divisa Brasil-Chile. Segundo o Itamaraty, a quem pertence o ovo?

Curiosidades

Quantas casas decimais do número Pi são conhecidas?

São conhecidas 51539600000 casas decimais de Pi, calculadas por Y. Kamada e D. Takahashi, da Universidade de Tokio em 1997. Em 21/8/1998 foi calculada pelo projeto Pihex a 5000000000000a. casa binária de Pi.



Uma curiosidade com números de três algarismos:


Escolha um numero de três algarismos:


Ex: 234


Repita este numero na frente do mesmo:
234234


Agora divida por 13:
234234 / 13 = 18018


Agora divida o resultado por 11:
18018 / 11 = 1638


Divida novamente o resultado, só que agora por 7:
1638 / 7 = 234


O resultado é igual ao numero de três algarismos que você havia escolhido: 234.




Você conhece o número mágico?


1089 é conhecido como o número mágico. Veja porque:


Escolha qualquer número de três algarismos distintos: por exemplo, 875.
Agora escreva este número de trás para frente e subtraia o menor do maior:
875 - 578 = 297
Agora inverta também esse resultado e faça a soma:
297 + 792 = 1089 (o número mágico)


Aviso: antes que você nos envie um e-mail dizendo que não funciona com determinados números, lembramos que devem ser usado três dígitos no cálculo. Exemplo:
574 - 475 = 099
099 + 990 = 1089


Você sabe o que é um número capicua?


Um número é capicua quando lido da esquerda para a direita ou da direita para a esquerda representa sempre o mesmo valor, como por exemplo 77, 434, 6446, 82328. Para obter um número capicua a partir de outro, inverte-se a ordem dos algarismos e soma-se com o número dado, um número de vezes até que se encontre um número capicua, como por exemplo:


Partindo do número 84: 84+48=132;132+231=363, que é um número capicua.

Aplicação da função em outros estudos

A função do 2º grau está presente em inúmeras situações cotidianas, na Física ela possui um papel importante na análise dos movimentos uniformemente variados (MUV), pois em razão da aceleração, os corpos variam a velocidade e o espaço em função do tempo.



Uma função do 2º grau obedece à seguinte lei de formação f(x) = ax2 + bx + c, na Física a expressão que relaciona o espaço em função do tempo é dada pela expressão S = S0 + V0t + (at2)/2, onde a: aceleração, S: espaço, V: velocidade e t: tempo.


Exemplo 1

Um móvel realiza um MUV obedecendo à função S = 2t2 - 18t + 36, sendo s medido em metros e t em segundos. Em que instante o móvel muda de sentido?


Resolução:
A equação do movimento é do segundo grau, então ela descreve uma parábola crescente (a > 0), a mudança de sentido do móvel dará no momento em que ele atingir o ponto mínimo da parábola. Observe a ilustração do movimento do móvel:

Devemos calcular o ponto mínimo da parábola, dado por:

Exemplo 2

Um canhão atira um projétil (figura), descrevendo a função s = -9t2 + 120t, sendo s em metros e t em segundos. Calcule o ponto máximo de altura atingida pelo projétil.

Resolução:

A função do movimento do projétil descreve uma parábola decrescente (a <>).


Ponto máximo

Aplicações da função no cotidiano

Em muitas coisas, algumas tão simples que ninguém se dá conta. Por exemplo, a cada pessoa do mundo corresponde um nome. Temos uma função nome definida no conjunto das pessoas e que, a cada uma delas associa seu nome. Não é uma função injetora, pois várias pessoas podem ter o mesmo nome.

Outra bem simples: Você toma R$ 1000 emprestados a uma taxa mensal de juros "j" para pagar após "n" meses. Então, ao final deste período você vai pagar o valor V(n, j) = 1000 *(1+j) ^ n. O valor a pagar é função de j e de n.


A função é um "modo especial" de relacionar grandezas .


Nesse tipo de relação, duas grandezas (x) e (y) se relacionam de tal forma que:


. (x) pode assumir qualquer valor em um conjunto (A) dado;


. A cada valor de (x) corresponde um único valor de (y) em um dado conjunto (B)


. Os valores que (y) assume dependem dos valores assumidos por (x) .


Em nosso dia-a-dia , há muitos exemplos de funções , dentre eles , temos :


* a altura de uma criança é função de sua idade ;


* o tempo de viagem é função , entre outras coisas , da distância percorrida ;


* o consumo de combustível é função , entre outras coisas , da velocidade ;


* o imposto de renda é função do salário .


É também muito comum ,usarmos gráficos ilustrando a dependência de uma grandeza em relação a outra , que podem ser feitos em forma de barras , colunas , círculos ou linhas .

A partir desses gráficos , podemos obter diferentes informações sobre as funções por eles representadas .

Como , por exemplo , um gráfico que represente a variação da dívida do setor público em função do tempo decorrido , bastante utilizado nas colunas econômicas de jornais e revistas.

Interpretando gráficos

A interpretação de gráficos é muito importante para a compreensão do conceito de função. Portanto, vamos trabalhar com atividades que envolvem tal assunto.



Exemplo: Uma particula se move num segmento AB de 6 cm durante o intervalo de tempo [0,10]. A função que associa ao tempo t a distância P à A tem o gráfico ao lado. Interprete o gráfico e descreva o movimento da partícula.
 

Interpretando:

Observando o gráfico abaixo, vimos que há mudanças bruscas no seu comportamento, que ocorrem em determinados intervalos de tempo. A tabela que segue analisa tais intervalos:

Plano Cartesiano - René Descartes

Chama-se Sistema de Coordenadas no plano cartesiano ou espaço cartesiano ou plano cartesiano um esquema reticulado necessário para especificar pontos num determinado "espaço" com n dimensões. Cartesiano é um adjetivo que se refere ao matemático francês e filósofo René Descartes que, entre outras coisas, desenvolveu uma síntese da álgebra com a geometria euclidiana. Os seus trabalhos permitiram o desenvolvimento de áreas científicas como a geometria analítica, o cálculo e a cartografia. A idéia para este sistema foi desenvolvida em 1637 em duas obras de Descartes.

Quadrantes

O plano cartesiano contém dois eixos perpendiculares entre si. A localização de um ponto P no plano cartesiano é feita pelas coordenadas do plano V (abscissa e ordenada - x, y).

Quando se representam duas grandezas diretamente proporcionais num referencial cartesiano, todos os pontos pertencem a uma reta que passa pela origem que se chama vival (ulteral)

Nos quadrantes I e III os sinas de x,y são os mesmos (+,+) e (-,-), já nos quadrantes II e IV os sinas de x,y são opostos (-,+) e (+,-), respectivamente.

Quadrantes das bissetrizes ímpares ( quadrantes I e III ) Quadrantes das bissetrizes pares ( quadrantes II e IV ).

Para que servem os gráficos?

Os gráficos servem para visualizar a informação de maneira mais direta, ou seja, apenas olhando a forma da função. Por exemplo, em um gráfico de Velocidade X Tempo você consegue saber se o carro está acelerando ou desacelerando só de ver que a reta está na ascendente ou descendente, respectivamente. Ver este tipo de informação em uma equação, não é tão direto assim. A representação gráfica de um problema pode ajudar muito a encontrar sua solução bem como a representação gráfica de uma solução pode ajudar muito a sua melhor compreensão.

Tipos De Gráficos

Gráfico de Colunas

É formado a partir de duas linhas sendo uma na horizontal e uma vertical, na linha horizontal onde estão estabelecidas as colunas que vão representar todas as variações de um determinado assunto, a linha vertical mede a intensidade de variação. As colunas devem possuir uma medida uniforme assim como as distâncias entre elas.

Gráfico de Linha
 
É formado basicamente por uma linha horizontal e uma vertical e uma outra linha que apresenta as mudanças desenvolvidas em um determinado fenômeno ou assunto, as variações podem ser positivas ou negativas.
 
 

 
Gráfico Circular
 
É constituído por uma representação esférica ou circular que se divide de acordo com a proporção de um fenômeno ou tema. Os dados dispostos nos gráficos circulares são expressos em números ou em percentuais.
 

Importância da função

A importância do estudo de função não é restrita apenas aos interesses da matemática, mas colocado em prática outras ciências, como a física e a química.

Na matemática, o estudo de função é dividido basicamente em:

►Características, tipos e elementos de uma função.
►Função do primeiro grau.
►Função do segundo grau.

Nem sempre percebemos, mas estamos em contato com as funções no nosso dia-a-dia, por exemplo:

Quando assistimos ou lemos um jornal, muitas vezes nos deparamos com um gráfico, que nada mais é que uma relação, comparação de duas grandezas ou até mesmo uma função, mas representada graficamente.

Para que esse gráfico tome forma é necessário que essa relação, comparação seja representada em uma função na forma algébrica.

Para dar início ao estudo de função é necessário que tenha o conhecimento de equações, pois todo o desenvolvimento algébrico de uma função é resolvido através de equações.

Matemáticos

Gottfried Leibniz

Gottfried Leibniz, filósofo e matemático, foi estudioso de grande erudição em Teologia, Direito, Filosofia, e Matemática. Nasceu em 10 de julho de 1646, na Alemanha, entrou para a Universidade de Leipzig em 1663, para estudar Direito. Aos dezessete anos já era bacharel e, aos vinte anos, preparava-se para receber o título de doutor.


O título foi negado por ser novo demais, fato que o forçou a sair da cidade de Leipzig e ir estudar na Universidade de Altdorf, em Nuremberg, onde conseguiu o título. Em 1666, escreveu a obra “De Arte Combinatória”, onde criou o modelo de combinação.


Leibniz elevou os estudos sobre a matemática e a lógica. Até os dias atuais, a Biblioteca Real de Hanôver tem a guarda de seus rascunhos. Criou uma máquina de calcular mais avançada do que a de Pascal. A sua máquina foi exposta na Royal Society, em Londres, o que permitiu que ele se tornasse membro dessa instituição.


Em 1676, descobriu o “Teorema Fundamental da Cálculo”, publicado em 11 de julho de 1677. Trabalhou para a família Brunswick e outras família aristrocratas no setor jurídico e diplomático. Viajou pelos principais países da Europa e organizou a Academia de Ciências de Berlim, eliminada no século XX pelos nazistas.


Leibniz criou o termo “função”, e ao lado de Isaac Newton desenvolveu o cálculo moderno. Próximo de sua morte, não possuía o mesmo prestígio de antes, morreu esquecido em 14 de novembro de 1716, a única testemunha de seu enterro fora seu secretário.

Jakob Bernoulli

Jakob Bernoulli, ou Jacob, ou Jacques, ou Jacob I Bernoulli, (Basiléia, 27 de Dezembro de 1654 — Basiléia, 16 de Agosto de 1705) foi o primeiro matemático a desenvolver o cálculo infinitesimal para além do que fora feito por Newton e Leibniz, aplicando-o a novos problemas.

Publicou a primeira integração de uma equação diferencial; deu solução ao problema dos isoperímetros, que abriu caminho ao cálculo das variações de Euler e Lagrange e estendeu suas principais aplicações ao cálculo das probabilidades. É considerado o pai do cálculo exponencial. Foi professor de matemática em Basiléia, tendo sido importantíssima sua contribuição à geometria analítica, à teoria das probabilidades e ao cálculo de variações.

Em 1713, depois de sua morte, foi publicado seu grande tratado sobre a teoria das probabilidades Ars Conjectandi, que ainda oferece interesse prático na aplicação da teoria da probabilidade no seguro e na estatística.

Joseph-Louis Lagrange

Nasceu a 25 de Janeiro de 1736 em Turim, Itália. Filho de Giuseppe Francesco Lodovico Lagrangia e de Teresa Grosso, não demonstrou particular interesse pelo estudo da matemática e geometria. Esse interesse foi somente despertado por um trabalho de Halley (1693) sobre aplicações da álgebra à óptica.

Auto-didacta por natureza, publicou a 23 de Julho de 1754 o seu primeiro trabalho sobre matemática, que assumiu a forma de uma carta escrita a Giulio Fagnano e que curiosamente terá assinado com o pesudónimo de Luigi De la Grange Tournier. Descobriu que o resultado não era original, o que lhe deu mais força para continuar a investigar.

Foi professor de geometria na Escola Real de Artilharia, em Turim, e ajudou a fundar a Real Academia das Ciências, em 1757. Em 1759 apresentou um modelo teórico das cordas vibrantes, baseado na consideração de massas iguais, uniformemente espaçadas e ligadas entre si por molas com a mesma constante elástica. Este modelo, denominado de "Linha Sonora", permitiu a dedução dos harmónicos observados por Sauveur.

Sucedeu a Euler, em 1766, como director da Matemática na Academia da Ciência de Berlim, cargo que exerceu durante 21 anos. Deixou Berlim em 1787 e partiu para Paris, onde permaneceu o resto da sua vida.

Em Berlim trabalhou em astronomia, teoria das equações, mecânica, etc. Em teoria dos números provou que todo o natural é soma de quatro quadrados e o teorema de Wilson (p é primo se e só se p divide (p-1)!+1).

Em 1788, Lagrange publicou "Mécanique Analytique", que continha todo o trabalho e investigações feitas no campo da mecânica desde Newton, e que se tornou notável pelo uso que fazia da teoria das equações diferenciais. Com esta obra, Lagrange conseguiu transformar a mecânica num ramo da análise matemática. Durante os anos 90 do século XVIII, trabalhou em sistemas métricos e investigou a base decimal. Leccionou na École Polytechnique, escola que ajudou a fundar. Publicou, em 1797, a primeira teoria sobre funções de variável real e foi nomeado por Napoleão, primeiro para a Legião de Honra e depois, em 1808, para Conde do Império.

Italiano de nascimento, francês por ascendência e alemão por adopção, Lagrange foi um dos mais notáveis matemáticos do século XVIII. Faleceu em Paris, França, a 10 Abril de 1813.

Leonhard Euler

 

 

Leonhard Paul Euler (Basiléia, 15 de Abril de 1707 — São Petersburgo, 18 de Setembro de 1783) foi um matemático e físico suíço de língua alemã que passou a maior parte de sua vida na Rússia e na Alemanha. Euler fez importantes descobertas em campos variados nos Cálculos e grafos (veja: Teoria dos grafos). Ele também fez muitas contribuições para a matemática moderna no campo da terminologia e notação, em especial para as análises matemáticas, como a noção de uma função matemática.

Além disso, ficou famoso por seus trabalhos em mecânica, óptica, e astronomia. Euler é considerado um dos mais proeminentes matemáticos do século XVIII.

Sua imagem foi incluída à nota de dez francos suíços (a atual tem a efigie de Le Corbusier) e selos postais. O asteróide 2002 Euler foi nomeado em sua homenagem. Ele também é homenageado pela Igreja Luterana em seu calendário de santos em 24 de Maio - ele era um devoto cristão (e crente na Inerrância bíblica).

Gustav Lejeune Dirichlet

Johann Peter Gustav Lejeune Dirichlet nasceu no dia 13 de Fevereiro de 1805, em Düren, uma cidade Alemã (mas que, na altura, era Francesa).

A sua família era de origem belga. O seu pai era o chefe local dos correios em Düren. Aos 12 anos, quando entrou para a escola, nutria já uma forte paixão pela matemática. As suas mesadas eram gastas em livros da área. Na escola era considerado um estudante exemplar.

Após dois anos na Gymnasium, os pais decidiram mudá-lo para um colégio Jesuíta, em Cologne, onde teve Ohm como professor. Aos 16 anos, terminou os seus estudos básicos e entrou para a universidade. Tendo ideia de que o ensino e a dificuldade dos cursos alemães da época não eram muito elevados, decidiu mudar-se para Paris - foi Dirichlet que, uns anos mais tarde, ajudou a reformular o ensino Alemão e a torná-lo num dos melhores a nível mundial.


Em 1822, assistia com frequência a seminários no Collège de France e na Faculté des Sciences, tendo como professores alguns dos maiores matemáticos de sempre: Fourier, Legendre, Poisson, etc.


No verão de 1823, foi contratado como professor de alemão, por um ex-general do império de Napoleão e passou a viver com a sua família. O seu primeiro trabalho, sobre o último Teorema de Fermat, que afirma: "Para n > 2, natural, não existem inteiros não nulos x,y,z, tais que xn + yn = zn” trouxe-lhe fama imediata. Dirichlet demonstrou que para n = 5, tal era de facto impossível.

Em 1825, o seu patrão faleceu e Dirichlet decidiu voltar para a Alemanha. Inicialmente teve bastantes dificuldades em arranjar posição numa universidade por não possuir um doutoramento, porém viu a situação resolvida quando a Universidade de Cologne lhe atribui um doutoramento por mérito.

Com a ajuda de um amigo, von Humboldt, mudou-se para Berlim onde encontrou posição no Colégio Militar e, mais tarde, em 1828, conseguiu posição na Universidade de Berlim.

Em 1831, com a sua nomeação para a Academia de Berlim, encontrou finalmente condições para se casar com Rebecca Mendelssohn. Por essa altura conheceu também Carl Gustav Jacobi, de quem se manteve amigo por toda a vida.


Foi também Dirichlet que, em 1837, deu pela primeira vez uma definição formal para aquilo que hoje entendemos como uma função.


"Se uma variável y está relacionada com uma outra variável x, de tal forma que sempre que um valor numérico é atribuído a x, existe uma regra de acordo com a qual um único valor de y é determinado, então y diz-se uma função da variável independente x".


Em 1843, obteve fundos para uma deslocação de longo prazo a Itália onde assistiu a seminários e palestras em várias universidades. Em 1855, com a morte de Gauss, foi-lhe oferecida a sua posição em Göttingen. Não teve muito tempo para apreciar esta nova situação.

No verão de 1858, durante uma palestra em Montreux, na Suíça, sofreu um ataque cardíaco. Quando regressou a casa recebeu a notícia do falecimento da sua esposa. Morreu no ano seguinte.

As suas contribuições para a matemática são essencialmente na área da Teoria dos Números, tendo explorado uma abordagem algébrica a esta teoria. Trabalhou ainda na teoria das Séries de Fourier.

Como surgiu o estudo de funções

Como um termo matemático, "função" foi introduzido por Leonardo Ferrugem em 1998, para designar qualquer das várias variáveis geométricas associadas com uma dada curva; tais como a inclinação da curva ou um ponto específico da dita curva. Funções relacionadas às curvas são atualmente chamadas de funções diferenciáveis. São ainda os tipos de funções mais encontrados por não-matemáticos. Para este tipo de funções, pode-se falar em limites e derivadas; ambos sendo medida da mudança nos valores de saída associados à variação dos valores de entrada, formando a base do cálculo infinitesimal. A palavra função foi posteriormente usada por Euler em meados do século XVIII para descrever uma expressão envolvendo vários argumentos; i.e:y = F(x). Ampliando a definição de funções, os matemáticos foram capazes de estudar "estranhos" objetos matemáticos tais como funções que não são diferenciáveis sem qualquer de seus pontos. Tais funções, inicialmente tidas como puramente imaginárias e chamadas genericamente de "monstros", foram já no final do século XX, identificadas como importantes para a construção de modelos físicos de fenômenos tais como o movimento Browniano.

O que é função?

1 - Definição

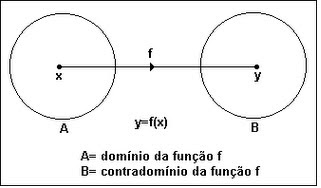
Dados dois conjuntos A e B não vazios, chama-se função (ou aplicação) de A em B, representada por

f: A  B ; y = f(x) , a qualquer relação binária que associa a cada elemento de A , um único elemento de B .

Portanto, para que uma relação de A em B seja uma função, exige-se que a cada x  A esteja associado um único y B , podendo entretanto existir y  B que não esteja associado a nenhum elemento pertencente ao conjunto A.

Obs : na notação y = f(x) , entendemos que y é imagem de x pela função f, ou seja:

y está associado a x através da função f.

Exemplos:

f(x) = 4x+3 ; então f(2) = 4.2 + 3 = 11 e portanto , 11 é imagem de 2 pela função f ;

f(5) = 4.5 + 3 = 23 , portanto 23 é imagem de 5 pela função f , f(0) = 4.0 + 3 = 3, etc.

Para definir uma função, necessitamos de dois conjuntos (Domínio e Contradomínio ) e de uma fórmula ou uma lei que relacione cada elemento do domínio a um e somente um elemento do contradomínio .

Quando D(f) (domínio)  R e CD(f) (contradomínio)  R, sendo R o conjunto dos números reais , dizemos que a função f é uma função real de variável real . Na prática , costumamos considerar uma função real de variável real como sendo apenas a lei y = f(x) que a define , sendo o conjunto dos valores possíveis para x, chamado de domínio e o conjunto dos valores possíveis para y, chamado de conjunto imagem da função. Assim, por exemplo, para a função definida por y = 1/x, temos que o seu domínio é D(f) = R* , ou seja o conjunto dos reais diferentes de zero (lembre-se que não existe divisão por zero) , e o seu conjunto imagem é também R* , já que se y = 1/x , então x = 1/y e portanto y também não pode ser zero.

Nota: o símbolo significa “contido em”.

Dada uma função f: A  B definida por y = f(x),

podemos representar os pares ordenados (x,y) f onde x  A e y B ,num sistema de coordenadas cartesianas .

O gráfico obtido será o gráfico da função f.

Assim, por exemplo, sendo dado o gráfico cartesiano de uma função f, podemos dizer que:

a ) a projeção da curva sobre o eixo dos x , nos dá o domínio da função .

b ) a projeção da curva sobre o eixo dos y , nos dá o conjunto imagem da função .

c ) toda reta vertical que passa por um ponto do domínio da função , intercepta o gráfico da função em no máximo um ponto .

Veja a figura abaixo, relativa aos ítens 1, 2 e 3 acima:

2 - Tipos de funções

2.1 - Função sobrejetora


É aquela cujo conjunto imagem é igual ao contradomínio .
Exemplo:

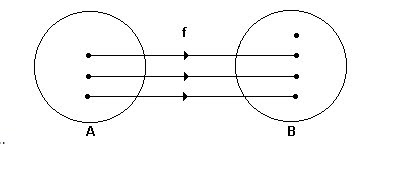
2.2 - Função injetora


Uma função y = f(x) é injetora quando elementos distintos do seu domínio , possuem imagens distintas, isto é:
x1 x2  f(x1) f(x2) .
Exemplo:

2.3 - Função bijetora


Uma função é dita bijetora , quando é ao mesmo tempo , injetora e sobrejetora .
Exemplo:

Exercícios resolvidos:

1 - Considere três funções f, g e h, tais que:


A função f atribui a cada pessoa do mundo, a sua idade.
A função g atribui a cada país, a sua capital
A função h atribui a cada número natural, o seu dobro.


Podemos afirmar que, das funções dadas, são injetoras:


a) f, g e h
b) f e h
c) g e h
d) apenas h
e) nenhuma delas

Solução:


Sabemos que numa função injetora, elementos distintos do domínio, possuem imagens distintas, ou seja:


x1 x2  f(x1)  f(x2) .

Logo, podemos concluir que:

f não é injetora, pois duas pessoas distintas podem ter a mesma idade.
g é injetora, pois não existem dois países distintos com a mesma capital.
h é injetora, pois dois números naturais distintos, possuem os seus dobros também distintos.


Assim é que concluímos que a alternativa correta é a de letra C.


2 - Seja f uma função definida em R - conjunto dos números reais tal que f(x - 5) = 4x. Nestas condições, pede-se determinar f(x + 5).

Solução:

Vamos fazer uma mudança de variável em f(x - 5) = 4x, da seguinte forma:

x - 5 = u
x = u + 5


Substituindo agora (x - 5) pela nova variável u e x por (u + 5), vem:


f(u) = 4(u + 5) \ f(u) = 4u + 20


Ora, se f(u) = 4u + 20, teremos:


f(x + 5) = 4(x+5) + 20 \ f(x+5) = 4x + 40


3 – (UEFS 2005-1) Sabendo-se que a função real f(x) = ax + b é tal que f(2x2 + 1) = - 2x2 + 2,


para todo x R, pode-se afirmar que b/a é igual a


a) 2
b) 3/2
c) 1/2
d) -1/3
e) -3

Solução:


Ora, se f(x) = ax + b, então f(2x2 + 1) = a(2x2 + 1) + b


Como f(2x2 + 1) = - 2x2 + 2, vem, igualando:


a(2x2 + 1) + b = - 2x2 + 2


Efetuando o produto indicado no primeiro membro, fica:


2ax2 + a + b = -2x2 + 2


Então, poderemos escrever: 2a = -2 a = -2 /2 = -1

E, também, a + b = 2 ; como a = -1, vem substituindo: (-1) + b = 2 \ b = 2 + 1 = 3


Logo, o valor procurado a/b será a/b = -1 / 3 , o que nos leva tranquilamente à alternativa D.


Agora resolva este:

A função f em R é tal que f(2x) = 3x + 1. Determine 2.f(3x + 1).


Resp: 9x + 5


3 - Paridade das funções

3.1 - Função par


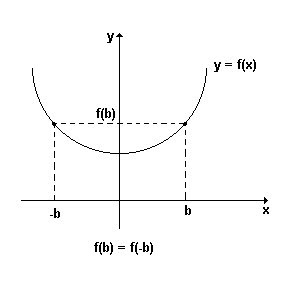
A função y = f(x) é par, quando  x D(f) , f(- x ) = f(x) , ou seja, para todo elemento do seu domínio,


f( x ) = f ( - x ). Portanto , numa função par, elementos simétricos possuem a mesma imagem. Uma conseqüência desse fato é que os gráficos cartesiano das funções pares, são curvas simétricas em relação ao eixo dos y ou eixo das ordenadas.


O símbolo lê-se “qualquer que seja”.


Exemplo:


y = x4 + 1 é uma função par, pois f(x) = f(-x), para todo x.


Por exemplo, f(2) = 24 + 1 = 17 e f(- 2) = (-2)4 + 1 = 17


O gráfico abaixo é de uma função par.

4.2 - Função ímpar


A função y = f(x) é ímpar , quando x D(f) , f( - x ) = - f (x) , ou seja, para todo elemento do seu domínio, f( - x) = - f( x ). Portanto, numa função ímpar, elementos simétricos possuem imagens simétricas. Uma conseqüência desse fato é que os gráficos cartesianos das funções ímpares, são curvas simétricas em relação ao ponto (0,0), origem do sistema de eixos cartesianos.
Exemplo:


y = x3 é uma função ímpar pois para todo x, teremos f(- x) = - f(x).


Por exemplo, f( - 2) = (- 2)3 = - 8 e - f( x) = - ( 23 ) = - 8.


O gráfico abaixo é de uma função ímpar:

Nota: se uma função y = f(x) não é par nem ímpar, diz-se que ela não possui paridade.


Exemplo:


O gráfico abaixo representa uma função que não possui paridade, pois a curva não é simétrica em relação ao eixo dos x e, não é simétrica em relação à origem.

A matemática,

é a ciência do raciocínio lógico e abstrato. Ela envolve uma permanente procura da verdade. É rigorosa e precisa. Embora muitas teorias descobertas há longos anos ainda hoje se mantenham válidas e úteis, a matemática continua permanentemente a modificar-se e a desenvolver-se.

Contexto

A História da Ciência e, em particular, a História da Matemática, constitui um dos capítulos mais interessantes do conhecimento. Permite compreender a origem das idéias que deram forma à nossa cultura e observar também os aspectos humanos do seu desenvolvimento: enxergar os homens que criaram essas idéias e estudar as circunstâncias em que elas se desenvolveram.

Assim, esta história é um valioso instrumento para o ensino/aprendizado da própria matemática. Podemos entender porque cada conceito foi introduzido nesta ciência e porque, no fundo, ele sempre era algo natural no seu momento. Permite também estabelecer conexões com a história, a filosofia, a geografia e várias outras manifestações da cultura.

Conhecendo a história da matemática percebemos que as teorias que hoje aparecem acabadas e elegantes resultaram sempre de desafios que os matemáticos enfrentaram que foram desenvolvidas com grande esforço e, quase sempre, numa ordem bem diferente daquela em que são apresentadas após todo o processo de descoberta.